Logique
Une fonction logique est une relation entre une ou plusieurs variables d’entrées et une seule variable de sortie. On réalise des opérations logiques (booléennes) sur une séquence de bits. Le bit est l’unité la plus simple dans un système de numération, ne pouvant prendre que deux valeurs, désignées le plus souvent par les chiffres 0 et 1
George Boole (1815 – 1864)
Il est le créateur de la logique moderne, que l’on appelle algèbre de Boole en son honneur.
Principe :
S’exprime au moyen de deux chiffres, on ne considère que deux états :
- la grandeur physique n’existe pas : 0
- la grandeur physique existe : 1
De nombreux dispositifs électroniques, électromécanique, mécaniques, électriques, pneumatiques, fonctionnement en tout ou rien. Ceci sous-entend qu’ils peuvent prendre 2 états. En voici quelques exemples :
- Arrêt marche,
- Ouvert fermé,
- Enclenché déclenché,
- Avant arrière,
- Vrai faux,
- Conduction blocage.
Notion de variable binaire
La variable logique est une grandeur qui peut prendre 2 valeurs qui sont repérées habituellement 0 ou 1.
On appelle cette grandeur un bit.
Cette variable est dite binaire et se note par une lettre comme en algèbre. Exemple : a, b, x
La variable binaire est aussi appelée variable booléenne.
Table de vérité
Une fonction X peut comporter n variables.
Pour chacune de ces combinaisons, la fonction peut prendre une valeur 0 ou 1.
Table de vérité avec une fonction ET
| a | b | a ET b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
De la base 10 (décimal) à la base 2 (binaire)
C’est simple, il suffit de savoir que 1+1=10…
Et oui, en binaire il n’existe pas de chiffres comme 2,3,4… Il n’y a que 1 et 0.
Calcul simple :
et ainsi de suite.
Tableau de 1 à 15
| Décimal | Binaire | Décimal | Binaire |
|---|---|---|---|
| 0 | 0000 | 8 | 1000 |
| 1 | 0001 | 9 | 1001 |
| 2 | 0010 | 10 | 1010 |
| 3 | 0011 | 11 | 1011 |
| 4 | 0100 | 12 | 1100 |
| 5 | 0101 | 13 | 1101 |
| 6 | 0110 | 14 | 1110 |
| 7 | 0111 | 15 | 1111 |
Exemples :
Les fonctions logiques de base
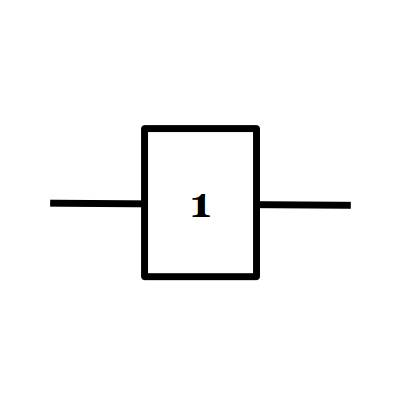
1/ La fonction OUI (us: buffer)
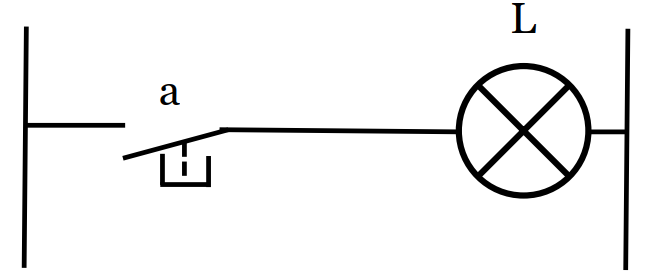
| a | L |
|---|---|
| 0 | 0 |
| 1 | 1 |


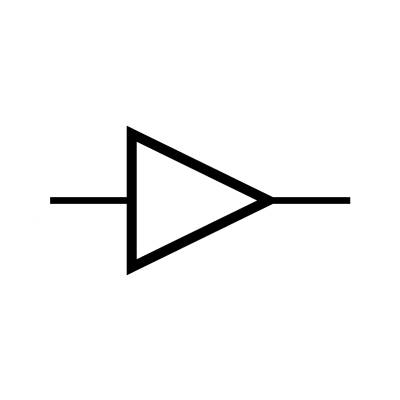
2/ La fonction NON (us: NOT)
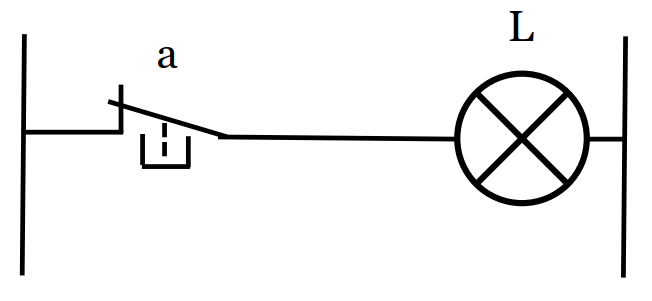
| a | L |
|---|---|
| 0 | 1 |
| 1 | 0 |

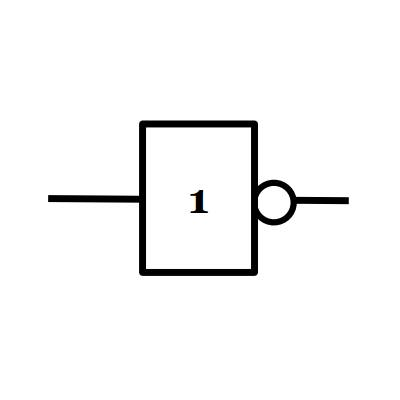

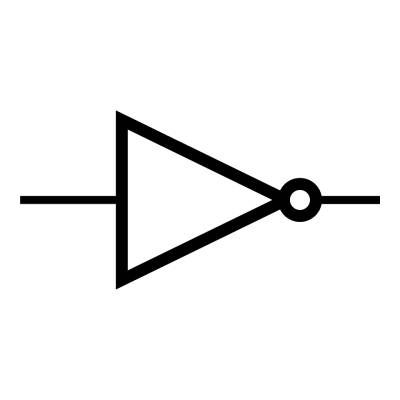
3/ La fonction OU (us: OR)
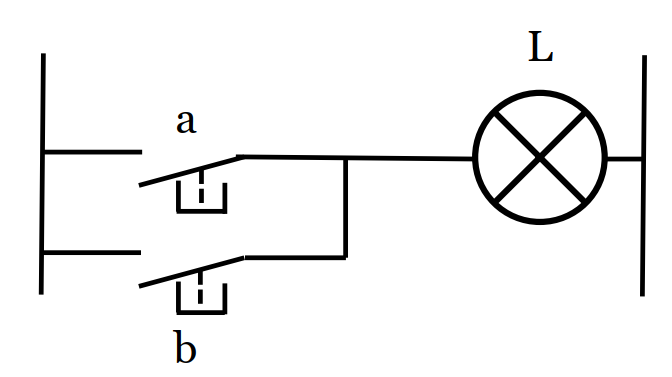
| a | b | L |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |

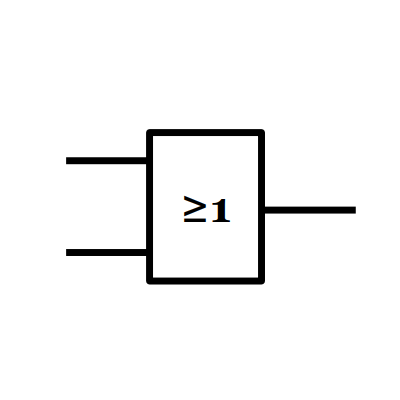

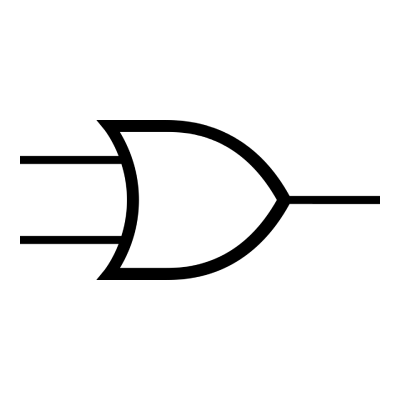
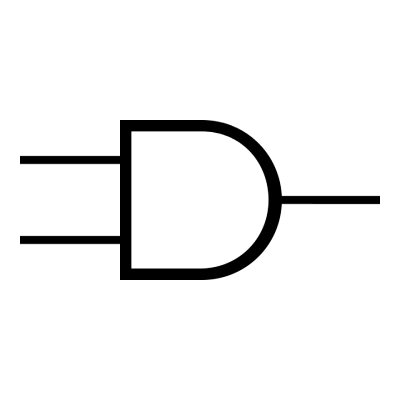
4/ La fonction ET (us: AND)
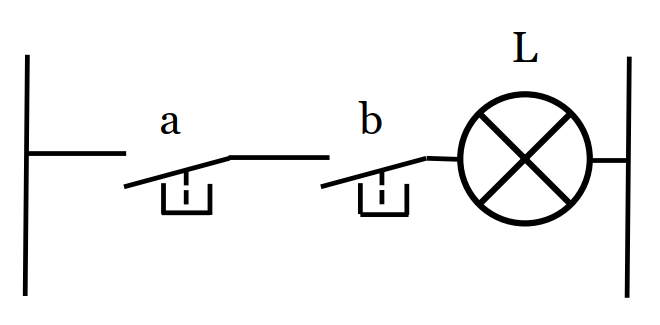
| a | b | L |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |

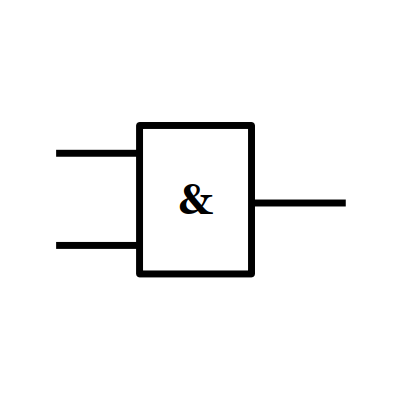

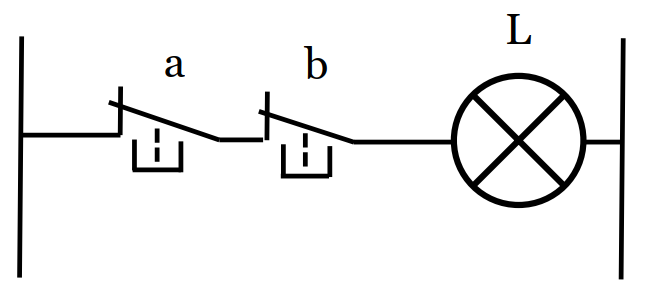
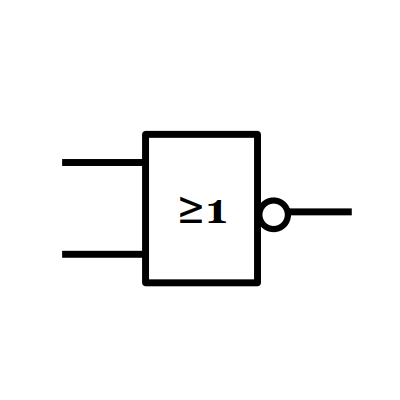
5/ La fonction NON OU (us: NOR)
| a | b | L |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |


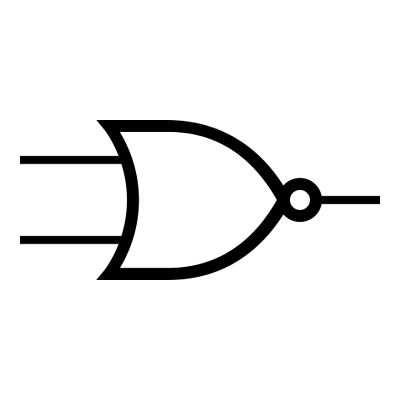
6/ La fonction NON ET (us: NAND)
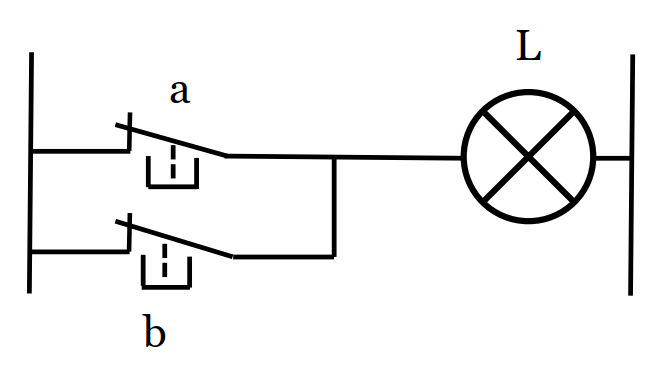
| a | b | L |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |

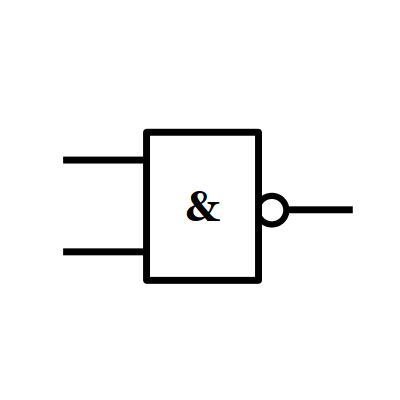

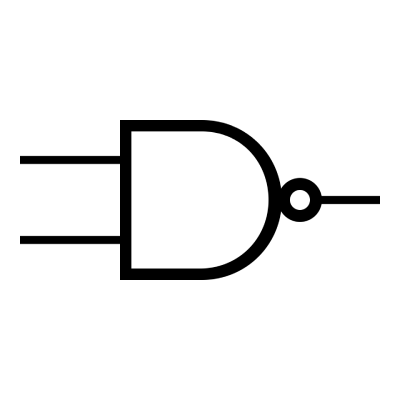
7/ La fonction OU EXCLUSIF (us: XOR)
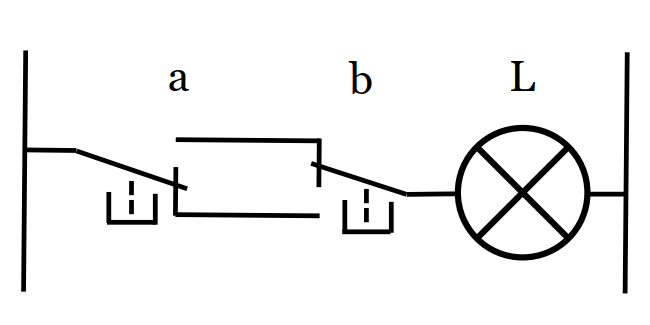
| a | b | L |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |

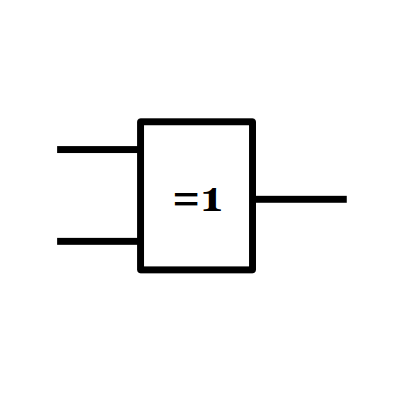

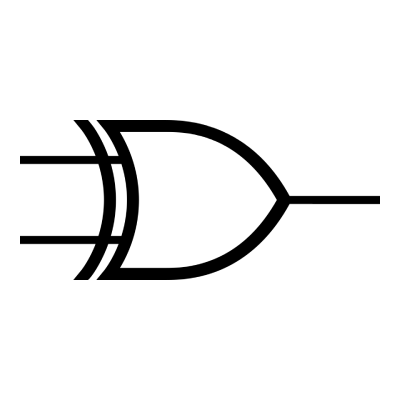
Il est possible de faire une simulation ici : https://logic.ly/demo/
Essayons de faire ce montage :
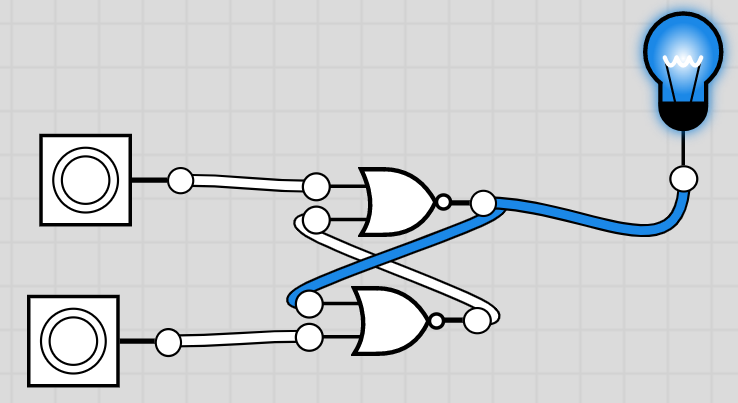
Vidéo :